Uji Asumsi Klasik Regresi: Contoh Kasus Uji Heteroskedastisitas + Analisis - Bagian II

Di bagian I pos sebelumnya, saya sudah membahas mengenai contoh soal dan uji heteroskedastisitas menggunakan uji glejser. Anda bisa baca pos-nya disini: Uji Asumsi Klasik Regresi: Contoh Kasus Uji Heteroskedastisitas + Analisis - Bagian II. Di bagian II pos ini, saya akan membahas output dan analisis interpretasi uji heteroskedastisitas. 

Kriteria pengujian glejser:

Ø  Nilai signifikansi antara variabel independen dengan absolute residual > 0.05 --> Tidak terjadi heteroskedastisitas

Ø  Nilai signifikansi antara variabel independen dengan absolute residual < 0.05 --> Terjadi heteroskedastisitas

Dapat dilihat pada output Coefficients pada nilai Sig yang menunjukkan tingkat signifikansi antara variabel independen dengan absolute residual (ABS_RES). Nilai signifikansi per variabel secara parsial dapat dijabarkan sebagai berikut:

·         Signifikansi biaya produksi dengan ABS_RES sebesar0.475

·         Signifikansi biaya distribusi dengan ABS_RES sebesar 0.946

·         Signifikansi biaya promosi dengan ABS_RES sebesar 0.736

Sig menunjukkan bahwa setiap variabel independen memilikinilai > 0.05, sehingga dapat disimpulkan bahwa model ini tidak mengalami masalah heteroskedastisitas. Atau dengan kata lain, tidak terjadi ketidaksamaan varians pada biaya produksi, biaya promosi dan biaya distribusi terhadap nilai absolute residual yang artinya model regresi memiliki varians yang sama.

Uji Scatter Plot

Alternatif uji tambahan pada uji heteroskedastisitas dapat dilakukan dengan menggunakan uji scatter plot. Uji scatter plot ini sifatnya hanyalah sebagai uji tambahn atau uji pendukung.  Langkah-langkah pengujian:

1. Pilih Menu à Analyze à Regression .. sehingga tampak tampilan di bawah

1. Klik tombol reset untuk menghapus seluruh input.. Pengisian:

Ø  Dependent. Masukkan variabel Tingkat Penjualan.

Ø  Independent(s). Masukkan Biaya Produksi, Biaya Distribusi, dan Biaya Promosi. Kemudian tekan Method dan pilih Enter. 

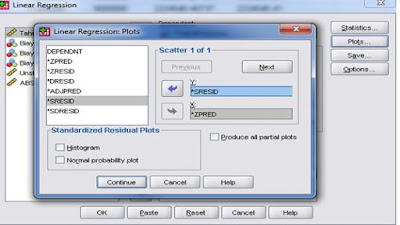
2. Tekan tomnol Plots. Pengisian:

Ø  Masukkan variabel SRESID pada sumbu (pilihan) Y.

Ø  Masukkan variabel ZPRED pada sumbu (pilihan) X.

SRESID berisi data residu (eror) yang telah distandardisasikan, sedangkan ZPRED adalah data hasil prediksi variabel dependen yang telah distandardisasikan. Sehingga grafik akan menampilkan hubungan eror dengan prediksi awalnya.

3. Abaikan bagian lain dan tekan Continue --> OK. Lalu muncul output seperti dibawah ini

Model regresi dapat dikatakan tidak terjadi heteroskedastisitas apabila memenuhi syarat-syarat sebagai berikut.

a.    Jika terdapat pola tertentu, seperti yang ada membentuk pola tertentu secara teratur (bergelombang, melebar kemudian menyempit), maka hal ini mengindikasikan telah terjadi heteroskedastisitas.

b.    Jika tidak ada pola yang jelas serta titik-titik menyebar di atas dan di bawah angka 0 pada sumbu Y, maka tidak terjadi heteroskedastisitas.

Dari grafik diatas, terlihat bahwa titik-titik menyebar secara acak dan tidak membentuk pola tertntu yang jelas. Titik-titik (plot) tersebar baik di atas maupun di bawah angka 0 pada sumbu Y. Artinya, pada kasus ini tidak terjadi heteroskedastisitas pada model regresi, sehingga model regresi layak digunakan untuk memprediksi Tingkat Penjualan berdasarkan masukan variabel independennya.